Chia VDF 算法原理剖析

随着爆火产品Chia的出现，挖矿行业又有了更新颖亲民的玩法，即低门槛的硬盘挖矿方式，这种挖矿方式让越来越多的普通人能够参与到挖矿中来，一起感受区块链行业的热潮。

根据Chia的白皮书介绍，Chia采用的共识机制是空间证明（POS, Proof Of Space）和时间证明(POT, Proof Of Time)。POS主要用来证明用户的确有未使用空间可以用来存储，而POT则用来保证整个系统的安全性，其主要算法是VDF 可验证延迟函数（Verifiable Delay Function），VDF得出的运算结果必须经历一定的时间，并且可以由网络中的任何节点快速认证，增加POS获得出块权的概率。

Verifiable：即经过一定次数的计算后，prover可以快速生成一个小的proof来证明计算有效性，verifier不用重复执行计算就可以得知计算的正确性；

Delay：即prover只有执行正确次数的计算后，才能得到正确的结果，不会出现没达到指定次数前，就得到正确结果的情况；

Function：即结果是确定性的，输入x，就会得到y。

Figure 1 POT

VDF的计算

基于Chia的设计模式，如果某个节点的VDF计算速度高于其他节点，有可能会发起某种安全攻击。因此，为了避免这一威胁，Chia希望节点中运行的VDF算法是最高效的，所以基本没有什么优化空间。为此，Chia还举办了两次VDF效率竞赛，以高额的奖励来吸引业内精英参与到本次活动中来，广泛汲取大家的智慧，来获取效率最高的VDF。

如上图所示，Chia里用到的VDF算法其实很简单，就是对一个数x进行连续的T次平方计算，x是一个未知阶的群组（a group of unknown order）的元素。为什么是未知阶的群组，其中缘由也很简单：

如果群组的阶为d，那么根据群组的性质：x2^T = x(2^T) % d

就会存在未达到指定次数T，就得到正确结果，这与Chia的设计不一致；因此，群组的阶是无法被知道的；生成未知阶的群组的方式有两种：

基于RSA的群；

虚二次域类群；

当选择基于RSA的方式时，群的阶N=pq，其中p、q都是很大的素数且不可公开，因此，计算这种群的阶的难度就和分解大数N一样困难。所以被认为是安全的，但是，这种方式需要可信设置，即p、q由可信第三方生成，或许也可以用MPC的方式，但是总之，它需要可信设置；

而基于虚二次域的类群可以消除可信设置，因为一个满足|d|=3 mod 4关系的负大素数生成的类群，计算其阶是困难的（为什么困难，将在另外一篇文章里详细阐述，涉及数学概念较多，将尽量写的简明易懂些），由于这个大素数可以公开，因此这种方式可以很容易的生成无须可信设置的未知阶的群。

了解了背后的数学概念，下面让我们再看一下，基于虚二次域类群的元素的平方应该如何计算，如下图所示（算法参考NUDUPL论文）：

Figure 2 if a < L

Figure 3 if a > L

NUDUPL算法为目前为止，计算虚二次域平方的最有效的方法，这也是在两次VDF算法竞赛中，参赛者们选用最多的方法。图2、图3展示了算法的两个主要分支，其中m = (a,b,c)、M = (A,B,C)都是群中元素的表示形式。

VDF的证明

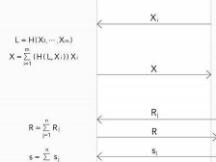
由图1可知，prover除了需要做T次计算外，还需要生成一个证明，来证明计算的正确性，关于VDF的正确性论证，这篇论文中给出了两个经典的方法，Chia采用的是Wesolowski的论证方法，此方法的过程如下图所示：

算法本身简单，且好理解。和论文中的Pietrzak算法相比，该算法生成证明更小，验证proof更快。

结 语

经过一段时间的研究和测试，Chia目前采用的VDF算法确实相当高效，从算法上，已经寻找不出可以大幅优化的点。“软的不行就来硬的”，这也是为什么我们仍然坚持把Chia的VDF算法研究的很深入的一个原因，目前已经着手硬件优化设计。从理论上讲，具有更高效率的VDF计算，可以获得更高的挖矿效率，这也是我们的目标。