一文了解如何攻克数据隐私保护问题?安全多方计算(MPC)来帮忙!
前言
安全多方计算一直以来被视为解决数据隐私保护问题的优选方案。万向区块链与生态合作伙伴矩阵元联合打造的基于隐私计算的新一代联盟区块链平台PlatONE就引入了安全多方计算,并结合态加密、零知识证明等密码学算法,实现数据多方安全共享。
安全多方计算如何在技术上帮助多方安全共享数据?这一技术方案具体在哪些场景拥有应用前景?本期万向区块链行业研究报告将从技术和应用两方面为大家解读安全多方计算。
本文作者为万向区块链首席经济学家办公室,在本微信公众号回复“行业研究”,可获取往期文章。
摘要
本文对安全多方计算做出技术及应用分析。结论是,安全多方计算能够解决互不信任的参与方之间保护隐私的协同计算问题。安全多方计算拓展了传统分布式计算的边界以及信息安全范畴,对解决网络环境下的信息安全具有重要价值。安全多方计算能够结合多行业领域进行数据融合,对数据市场的发展十分重要。
关键词: 安全多方计算、数据、隐私
数据是一个复杂概念,有多种类型和丰富特征。随着时代从互联网转变至区块链,数据即将成为可产生经济价值的资产。但是,大多数企业考虑到数据安全和个人隐私等问题,对数据共享都非常谨慎。对个人数据而言,控制权和隐私保护的重要性超过所有权。因此,企业在面临数据输入的隐私及输出的结果上常常遇到平衡上的困难。举例来说: 医院需要与保险公司分享病患数据,但是又不能泄露病患的个人隐私。安全多方计算(Secure Muti-party Computation)提供了一种技术上的解决方案,能够在无可信第三方的情况下安全地进行多方协同的计算。本文分为三个部分: 第一部分探讨安全多方计算的架构。第二部分研究安全多方计算的技术实现方式。第三部分分析安全多方计算应用及未来发展。
一、
安全多方计算
(一) 定义
安全多方计算可以定义为在一个分布式网络且不存在可信第三方的情况下,多个参与实体各自持有秘密输入,并希望共同完成对某函数的计算并得到结果,前提是要求每个参与实体均不能得知除自身外其他参与实体任何输入信息。
以下为安全多方计算的数学表述:有n个参与实体

,要以一种隐私保护的方式共同计算一个函数,所谓的隐私保护是指输出结果的正确性和输入信息、输出信息的保密性。每个参与实体

,有一个自己的秘密输入信息

,n 个参与实体要共同计算一个函数


,

为参与实体分别得知的运算结果。计算结束时,每个参与实体

只能得知

, 不能获得其他参与实体的任何信息。
(二) 安全多方计算架构
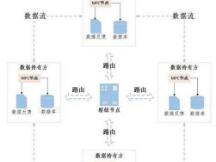
安全多方计算主要分为两个参与方:参与节点及枢纽节点。各个参与节点地位相同,可以发起协同计算任务,也可以选择参与其他方发起的计算任务。枢纽节点不参与实际协同计算,主要用于控制传输网络、路由寻址及计算逻辑传输。此外,在去中心化的网络拓扑里,枢纽节点是可以删减的,参与节点可以与其他参与节点进行点到点连接,直接完成协同计算。
安全多方计算过程中,每个数据持有方可发起协同计算任务,并通过枢纽节点进行路由寻址,选择相似数据类型的其余数据持有方进行安全的协同计算。参与协同计算的多个数据持有方的参与节点会根据计算逻辑,从本地数据库中查询所需数据,共同就安全多方计算任务在密态数据流间进行协同计算。整个过程各方的明文数据全部在本地存储,并不会提供给其他节点。在保证数据隐私的情况下,枢纽节点将计算结果输出至整个计算任务系统, 从而各方得到正确的数据结果。
安全多方计算主要有三个特性: 第一是隐私性。安全多方计算首要的目的是各参与方在协作计算时如何对隐私数据进行保护,即在计算过程中必须保证各方私密输入独立,计算时不泄露任何本地数据。第二是正确性。多方计算参与各方通过约定安全多方计算协议发起计算任务并进行协同计算,运算数据结果具备正确性。第三是去中心化。安全多方计算中,各参与方地位平等,不存在任何有特权的参与方或第三方,提供一种去中心化的计算模式。

图1:安全多方计算技术框架图 来源: 链闻
(三) 安全多方计算信任环境
安全多方计算的信任环境或者说整体安全定义通常由真实-理想模型(Real-Ideal Paradigm)来表达。在真实-理想模型中,存在一个虚拟的“理想”环境,与真实环境进行比较。在理想环境里,所有参与方都会将各自的秘密数据发送给一个可信第三方,由可信第三方完成计算。而在真实环境下,不存在这样的可信第三方,所有参与方通过互相交换信息,完成协同计算,并且会存在敌手进行控制其中部分参与方的情况。一个安全多方计算系统满足在真实-理想模型下的安全性,是指真实环境下的敌手无法产生比理想环境下的攻击者更多的危害;换言之,如果存在敌手可以对真实环境造成危害,那么也存在敌手可以对理想环境造成同等效果的危害。由逆否命题可知,事实上,不存在敌手能对理想环境造成危害,从而可以得出结论:不存在真实环境下的成功的敌手。
一般而言,在安全多方计算中,根据攻击者的能力差异可以定义两种不同的攻击者相关的安全模型。第一,半诚实模型(Semi-Honest Adversaries’ Security)。在半诚实行为模型中,假设敌手会诚实地参与安全多方计算的具体协议,遵照协议的每一步进行,但是会试图通过从协议执行过程中获取的内容来推测他方的隐私。第二,恶意行为模型(Malicious Adversaries’ Security)。在恶意行为模型中,恶意节点可能会不遵循协议,采取任意的行为(例如伪造消息或者拒绝响应)获取他方的隐私。
目前有许多安全多方计算的改进方案,可以达到恶意行为模型下的安全性,但是都需要付出很大的性能代价,大规模的安全多方计算产品,基本上通常只考虑半诚实模型,恶意行为模型的解决方案会严重影响效率和实用性。
二、
安全多方计算的实现形式
(一) 秘密共享
秘密共享是在一个常被应用在多方安全签名的技术,它主要用于保护重要信息被丢失、或篡改。通过秘密共享机制,秘密信息会被拆分,每个参与者仅持有该秘密的一部分,个人持有部分碎片无法用于恢复秘密,需要凑齐预定数量 (或门限) 的碎片。假设多方安全签名中存在一个秘密 S作为签名的私钥,将秘密S进行特定运算,得到w个秘密碎片

,交给 w个人保存,当至少t个人同时拿出自己所拥有的秘密碎片

时,即可还原出最初的秘密S,t则为秘密共享设定的预订门限,少于t个参与者则无人能够得到秘密S。
(二) 不经意传输(Oblivious Transfer)
不经意传输是一种密码学协议,被广泛应用于安全多方计算领域,它解决了以下问题: 假设 Alice 有两个数值

和

,Bob 想知道其中的一个数值

。通过不经意传输Bob可以知道

,但不知道

,同时Alice不知道i。举例来说,Alice 手上有两组密封的密码组合,Bob只能获得一组密码且Bob希望Alice不知道他选择哪一组密码。这时候就能利用不经意传输来完成交易。

图2: 不经意传输示意图 来源: 链闻
不经意传输存在双方角色,发送者与接收者。一个可行的具体实现过程,分为四个步骤:条件假设接收者希望知道结果

,但不希望发送人知道他想要的是

。第一,发送者生成两对不同的公私钥,并公开两个公钥

及

。第二,接收者会生成一个随机数k,再用

对k进行加密,传给发送者。第三,发送者用他的两个私钥及对这个加密后的进行解密,用

解密得到随机数

,用

解密得到随机数

。

和

相等,而

则为一无关的随机数。但发送者不知道接收人加密时用的哪个公钥,因此他不知道他算出来的哪个k正确。第四,发送者把

和

及

和

分别进行异或,把两个异或值传给接收者。接收者只能算出

而无法推测出

,同时发送人也无法知道他能算出哪一个结果。
(三) 混淆电路(Garbled Circuit)
混淆电路是姚期智教授在80年代提出的安全多方计算概念。混淆电路是一种密码学协议,遵照这个协议,两个参与方能在互相不知晓对方数据的情况下计算某一函数。举姚氏百万富翁问题(Yao's Millionaires' Problem) 为例,两个百万富翁 Alice和 Bob 想在不知道对方精准财富值的情况下比较谁的财富值更高。比如 Alice 的财富值是 20,Bob 的财富值是 15。藉由混淆电路,Alice和 Bob 都可以知道谁更富有,但是 Alice 和 Bob 都不知道对方的财富值。混淆电路的核心逻辑是先将计算问题转换为由与门、或门、非门所组成的布尔逻辑电路,再通过公钥加密、不经意传输等技术来扰乱这些电路值以掩盖信息,在整个过程双方传输的都是密码或随机数,不会有任何有效信息泄露。因此双方在得到计算结果的同时,达到了对隐私数据数据保护的目的。
假设存在双方Alice及Bob进行混淆电路协议。混淆电路实现过程分为四个步骤: 第一,Alice生成混淆电路。由图4可知,Alice生成的混淆电路中间会连接许多逻辑门,每个逻辑门都有输入线及输出线,且都有一组真值表(Truth table)。第二,Alice与Bob通信。Alice将逻辑门的真值表对称加密并将真值表的行列打乱成混淆表(Garbled table)传送至Bob。第三,Bob在接收到加密真值表后,对加密真值表的每一行进行解密,最终只有一行能解密成功,并提取相关的加密信息。其中,Bob 通过不经意传输协议从 Alice 获得对应的解密字符串。不经意传输能够保证Bob获得对应的解密字符串,且Alce无法得知Bob获得哪一个。最后,Bob将计算结果返回给Alice,双方共享计算结果。由于双方需对电路中每个逻辑门进行几个对称密钥操作,因此使用混淆电路的方案的计算复杂度相对也较高,并且当扩展到参与方较多的计算场景时会更加复杂。

图3: 一般电路、门及真值表 来源: 安全计算与密码学
(四) 零知识证明
零知识证明指的是示证者能够在不向验证者提供任何有用的信息的情况下,使验证者相信某个论断是正确的。零知识证明存在双方或多方角色: 示证者(prover)与验证者(verifier)。示证者宣称某一命题为真,而验证者确认该命题是否为真。
经典的零知识证明(Sigma协议)通常包含三个步骤: 第一,示证者先根据命题内容向验证者发送命题论述,这个论述必需经过处理转换成密态论述(一般称为“承诺”),且命题内容无法在后续的某一时刻进行篡改和抵赖。第二,验证者随机生成一个挑战并发给示证者。第三,示证者根据挑战和命题论述生成证明信息发给验证者。验证者利用证明信息判断示证者是否通过了该次挑战。重复多次这三个步骤,可以降低示证者是因为运气的成份通过挑战的概率。示证者提供的密态命题论述有两个作用,一来可以防止示证方对命题内容临时造假,二来可以让验证者无法得知全部信息,保持隐私性。
零知识证明具备三个属性: 第一,完备性。如果论述命题确实为真,那么诚实的验证者一定会被诚实的示证者说服。第二,可靠性,如果论述命题为假,那么示证者只能以很小的机率欺骗诚实的验证者。第三,零知识。验证者只能知道论述命题是否为真这一结果,而无法从整个交互式证明过程里获得其它任何有用的讯息。安全多方计算通常会利用零知识证明作为辅助手段,举例来说,验证恶意节点发送虚假数据或是做节点身份证明等等。
三、
安全多方计算应用与困难
目前来说,安全多方计算主要是通过混淆电路及秘密共享两个方式实现。基于混淆电路的协议更适用于两方逻辑运算,通讯负担较低,但拓展性较差。而基于秘密分享的安全多方计算其拓展性较强,支持无限多方参与计算,计算效率高,但通讯负载较大。目前安全多方计算的应用可以分为两个部分: 数据融合及数据资产化。
(一) 数据融合
让双方或多方数据融合并合作是目前安全多方计算能够发挥最大价值之处。举例来说,联合征信。银行拥有用户金融行为相关数据,而互联网公司一般拥有用户网络的使用数据,如何让两方的数据合作,共同建立一个信用模型,是数据协作的一个关键的问题。利用安全多方计算,可以在双方保留隐私的情况下找到共用的数据集,并且在多方数据基础上训练出的信用模型将更加准确,从而对未知情形提供更加合理的预测,减少数据融合的外部性。除此之外,数据安全存储也是一大应用。企业可使用秘密共享技术将数据以秘密的方式存储,有效防止内部人员非法盗用数据的情况发生。同时,存储的数据无需解密即可进行其他计算,既保证了安全性,又提升了计算效率。
(二) 数据资产化
安全多方计算有机会能够促进未来数据资产化及数据市场的发展。由于安全多方计算能够在数据传输的过程中从技术层面保证数据确权的问题,使数据的所有权与使用权划清界线,因此企业或个人将可以通过安全多方计算将有价值的数据视为资产,并在市场上流动或进行交易。数据提供方可以规定数据的用途、用量、有效期等使用属性,数据的使用者在拿到数据后只能在授权范围内合理地使用数据,并能将剩余数据的使用权量化或做进一步流通。安全多方计算可以将数据市场的本质由数据所有权转向数据使用权,保障原始数据所有者的权益,有效遏制原始数据泄漏,降低数据泄漏引起的数据流通风险,促进数据的大规模应用。
(三) 未来挑战
随着区块链和大数据等技术的逐渐发展,我们对数据及计算的要求相对更高。比如:区块链要求匿名性,数据计算需要隐私保护等等。因此类似安全多方计算等密码学技术在实际使用过程中,就会出现解释成本非常高,且效率低的问题。
安全多方计算会涉及庞大的计算量及通信量,尤其是涉及公钥运算。目前安全多方计算单个运算可以达到毫秒级,也就是说每秒钟最多能做几百次计算。但是在大数据的场景下,一个数据应用或模型训练往往涉及数十万单位的数据样本及特征量,运算效率会是一个问题。除此之外,对于某些在线或需要实时计算并且计算任务较复杂的应用场景,安全多方计算目前可能难以负担。示

微信掃描關注公眾號,及時掌握新動向
2.本文版權歸屬原作所有,僅代表作者本人觀點,不代表比特範的觀點或立場
2.本文版權歸屬原作所有,僅代表作者本人觀點,不代表比特範的觀點或立場