挖矿与经济博弈

比特范阅读 285 2020-4-16 17:00

技术最初是为比特币设计的一种特殊数据库技术, 它基于密码学中的椭圆曲线数字签名算法来实现去中心化的P2P系统设计.但区块链的作用不仅仅局限于比特币.现在人们在使用区块链这个词时, 有时是指数据结构, 有时是指数据库, 有时则是指数据库技术.从数据的角度来看, 区块链是一种分布式数据库(或称为分布式共享总账, Distributed shared ledger), 这里的“分布式”不仅体现为数据的分布式存储, 也体现为数据的分布式记录(即由系统参与者集体维护); 从记录效果的角度来看, 区块链可以生成一套记录时间先后、不可篡改、可信任的数据库, 这套数据库是去中心化存储且数据安全能够得到有效保证.具体地说, 区块链技术就是一种大家共同参与记录信息和存储信息的技术.过去, 人们将数据记录和存储的工作交给中心化的机构来完成, 而区块链技术则让系统中的每一个人都可以参与数据的记录和存储.区块链技术在没有中央控制点的分布式对等网络下, 使用分布式集体运作的方法, 构建了一个P2P的自组织网络.通过复杂的校验机制, 区块链数据库能够保持完整性、连续性和一致性, 即使部分参与人作假也无法改变区块链的完整性, 更无法篡改区块链中的数据.区块链技术涉及的关键点包括:去中心化(Decentralized)、去信任(Trustless)、集体维护(Collectively maintain)、可靠数据库(Reliable data base)、时间戳(Time stamp)、非对称加密(Asymmetric cryptography)等.

区块链技术原理的来源可归纳为数学上的拜占庭将军问题.将拜占庭将军问题延伸到互联网生活中来, 其内涵可概括为:在互联网大背景下, 当需要与不熟悉的对手进行价值交换活动时, 人们如何才能防止不会被其中的恶意破坏者欺骗和迷惑, 从而做出错误的决策.而如果进一步将拜占庭将军问题延伸到技术领域中来, 其内涵可概括为:在缺少可信任的中央节点和可信任通道的情况下, 分布在网络中的各个节点应如何达成共识.从这些角度来看, 区块链技术解决了闻名已久的拜占庭将军问题, 它提供了一种无需信任单个节点, 还能创建共识网络的方法.

作为区块链技术最成功的应用, 比特币系统应用工作量证明(Proof of work, PoW)的共识机制实现交易的不可篡改性和不可伪造性. PoW共识机制的核心思想是通过引入分布式节点的算力竞争来保证数据的一致性和共识的安全性.比特币系统中, 各节点基于各自的算力相互竞争, 共同解决一个求解复杂但验证容易的SHA256数学难题, 最快解决该难题的节点将获得区块记账权和系统自动生成的比特币奖励.具体过程如下:如果想产生一个区块并写入到区块链中, 需要找到一个小于系统规定难度值的随机数, 这样才可能被其他节点认可, 并写入到区块链中.而找到随机数需要输出密码散列函数家族SHA256的哈希算法.其中, 一个符合要求的输出值由N个前导零构成.零的个数取决于网络的难度值, 挖矿难度越高, 零的个数会越多.当输出值不满足要求时, 这个随机数就会增加一个单位, 直到找到为止.找到合适随机数后, 节点获得记账权和相应比特币奖励, 并将该过程中产生的所有交易记录在区块上, 所有区块按时间顺序连接则构成区块链.一般地, 比特币系统通过灵活调整随机数搜索的难度值来控制区块的平均生成时间.

在比特币系统中, 产生区块的过程称为挖矿, 进行挖矿的参与者称为矿工.由于比特币系统大约每10分钟产生一个区块, 这意味着大部分矿工在一定时间内很难产生区块.为了增加获得稳定收益的可能性, 矿工会选择加入开放矿池进行合作挖矿.具体地, 矿池中的矿工需要耗费资源尝试产生区块, 即发送完整工作量证明给管理者.但完整工作量很难产生, 矿工也可以选择发送部分工作量证明获得相应收益.无论哪个矿工产生区块, 获得的收益将按贡献比例分配给每个矿工.参与者注册为矿工很简单, 只需要提供一个公共的网络接口就可以加入开放矿池, 因此开放矿池很容易受到攻击.有些注册矿工只发送部分工作量证明, 当产生完整工作量证明时就会将其抛弃, 这种攻击方式被称为区块截留攻击.在这种情形下, 攻击者发送部分工作量证明, 但不会对矿池产生有效收益, 这也导致攻击者与其他矿工共同分享矿池收益, 从而减少其矿池的收益.

研究表明, 在一个开放的矿池中, 矿工可以通过攻击其他矿工增加自己的收益.如果所有矿工都选择攻击对方, 那么他们获得的收益将少于他们互不攻击时获得的收益.这就是PoW共识算法中的挖矿困境, 而这种困境也对应到博弈论中经典的囚徒困境(Prisoner's dilemma), 即攻击对个体而言是最优策略, 但却不是系统最优的.如何理解和分析挖矿过程中的博弈困境无疑给比特币的发展和技术开发乃至投入使用提供了理论基础.例如Eyal基于博弈理论, 定性地分析了挖矿过程中的困境, 但并没有给出纯策略存在条件以及相应证明.本文在文献的基础上进一步分析矿工博弈困境的纯策略和混合策略均衡, 并给出两种均衡存在的条件.

更为重要的是, PoW共识机制存在着显著的缺陷, 其强大算力造成的资源浪费(例如算力)历来为研究者所诟病, 而且长达10分钟的交易确认时间使其相对不适合小额交易的商业应用.与此同时, 随着区块链技术的发展和各种数字币的相继涌现, 研究者提出多种不依赖算力而能够达成共识的机制, 例如权益证明(Proof of stake, PoS)共识, 授权股份证明机制(Delegated proof of stake, DPoS)共识, 缠结(Tangle)以及Tendermint机制等.而最理想的共识算法是系统中的节点达成的共识是一个纳什均衡, 即单方面改变自己的策略都不会提高自身的收益.这为基于博弈论构建共识机制提供了新的思路.另一方面, PoW共识过程中的挖矿困境对应经典的囚徒困境模型, 其纳什均衡为互相攻击, 此时的系统收益并不能达到最优.为提高系统的整体效益, 有必要建立相关机制, 使矿工趋向于合作, 以获得较高的系统收益, 从而为实现高效的共识算法提供依据.

零行列式(Zero determinant, ZD)策略是近几年在博弈论中兴起的一种新方法, 它能够打破传统的纳什均衡理论.如Press和Dyson用ZD策略优化囚徒困境模型, 一方面可以解决系统收益低问题, 另一方面, 无论对手采取何种策略, 都可以强迫对手与自己收益之间满足线性关系.此外, ZD策略被应用到无线网络中的资源管理和频谱共享等问题.这些都为本文运用ZD策略对矿工的策略选择进行优化提供了参考和借鉴.

本文组织结构为:第1节介绍区块截留攻击和博弈理论中的纳什均衡及囚徒困境模型; 第2节利用博弈均衡理论对矿工算力相同和不相同两种情形的挖矿困境进行分析, 给出纯策略均衡以及混合策略均衡存在条件; 第3节运用ZD策略对区块截留攻击博弈进行优化, 得到获得较高系统收益时矿工策略选择的优化条件; 第4节给出数值仿真; 第5节总结本文内容, 并对今后工作进行展望.

1 预备知识

1.1 区块截留攻击

区块截留攻击是指在一个开放矿池中矿工与矿工之间的攻击.攻击者只发送部分工作量证明给矿池管理员, 当发现完整工作量证明时就将其抛弃.而工作量证明只能被任务的创建者使用, 攻击者不能将区块截留攻击的算力用于其他用途, 也不能从这部分算力中获得任何其他的收益.因此, 这种攻击一方面会造成算力浪费, 另一方面也会使整个矿池收益降低.此外, 少量部分工作量证明不会在很大程度上影响矿池的有效算力和有效收益, 但矿工进行攻击后, 整个矿池的有效算力和有效收益将低于所有矿工正常挖矿时所获得的收益.虽然矿池管理员检测到整个矿池的总收益降低, 发现正在遭受区块截留攻击, 但并不能判断哪个矿工正在发起攻击.

除了区块截留攻击, 还有其他几种类型的攻击, 例如矿池间的区块截留攻击、自私挖矿攻击、劫持攻击以及服务拒绝攻击等.

1.2 博弈理论

博弈论被誉为“社会科学中的数学”, 是研究具有斗争或竞争条件下最优决策问题的数学理论和方法.更确切地说, 是指在双方相互竞争对立的环境条件下, 参与者依靠所掌握的信息, 遵循一定的规则约束, 各自选择策略并取得相应的结果(或收益)的过程.

1.2.1 纳什均衡

通常认为Neumann与Morgenstern在1944年合著的《博弈论与经济行为》标志着现代博弈理论的初步形成.由此延续, 在上世纪50年代, 纳什提出了纳什均衡(Nash equilibrium, NE)理论, 刻画了所有博弈者策略构成的一种最优情势(Profile), 即任何博弈者单方面试图改变自己的策略, 则在该情势下该博弈者的收益将受到损害(至少不会改善).换言之, 这种情势下所有博弈者的策略都是所有其他对手策略的最优反应(Best response).

考虑n人博弈模型, 其策略空间为S=∏SiS=∏Si, SiSi是策略xixi的集合.定义X=(x1,x2,⋯,xn)X=(x1,x2,⋯,xn), xi∈Sixi∈Si, x−i=(x1,x2,⋯,xi−1,xi+1,⋯,xn)x−i=(x1,x2,⋯,xi−1,xi+1,⋯,xn).设Ui(X)Ui(X) = Ui(xi,x−i)Ui(xi,x−i)是个体i采取策略xixi时的收益函数. n个参与者在相互作用过程中可以达到纳什均衡X∗X∗ = (x∗1,x∗2,⋯,x∗n)(x1∗,x2∗,⋯,xn∗).这种均衡是指没有个体可以通过单方面改变自己的策略而增加收益, 即

∀i, Ui(x∗i,x∗−1)≥Ui(x′i,x∗−i), x∗i∈X∗; x′i∉X∗∀i, Ui(xi∗,x−1∗)≥Ui(xi′,x−i∗), xi∗∈X∗; xi′∉X∗

(1)

如果式(1) 对每个x′i∉x∗ixi′∉xi∗都严格成立, 称该均衡为严格纳什均衡.如果x∗ixi∗是一个纯策略, 称这个均衡为纯策略纳什均衡; 否则, 称这个均衡为混合纳什均衡.

1.2.2 囚徒困境博弈模型

考虑两个策略A和B的博弈模型, 当两个个体都采用A时, 各自获得奖励R; 当两者都采用B时, 各自获得惩罚P; 当A策略个体遇到B策略个体时, 前者收益为S, 后者收益为T.其收益矩阵表示如下:

ABAB(RTSP)ABAB(RSTP)

(2)

其中, R表示对“双方合作的奖励” (Reward for mutual cooperation), P表示对“双方背叛的惩罚” (Punishment for mutual defection), 当一方合作而另一方背叛时, S表示合作者获得“傻瓜的报酬” (Sucker′′s payoff), T表示背叛者获得“背叛的诱惑” (Temptation to defect).

囚徒困境模型是博弈论中最为经典的博弈模型.其背景如下:两个嫌疑犯P1P1和P2P2作案后被捕, 接受隔离审讯; 如果两人都坦白则各判8年, 如果一人坦白另一人不坦白, 坦白一方获释, 另一方判10年; 如果两人同时抗拒则因证据不足各判1年.对于P1P1和P2P2来说, 坦白意味着背叛(Defect), 不坦白意味着合作(Cooperate), 用收益矩阵表示如式(2), 满足条件T>R>P>ST>R>P>S, 且2R>T+S2R>T+S.对于行参与者而言, 如果列参与者选择合作, 则他的最优选择为背叛; 如果列参与者选择背叛, 背叛对手的收益高于合作时获得的收益.因此, 无论对手采用何种策略, 选择背叛策略都是最优的.理性个体最终会处于互相背叛状态, 即(D,D)(D,D)是囚徒困境博弈的纳什均衡状态.但是, 根据收益间的数值关系可知, 该状态的收益将低于两者选择合作时的收益, 理性参与者将面临选择合作或背叛的困境.

参与者进行一次交互, 会面临囚徒困境, 选择纳什均衡点---背叛.当进行多次博弈时, 就构成迭代的囚徒困境(Iterated prison′′s dilemma, IPD), 这时, 参与者最优策略依赖于对手策略选择, 从而改变原先的均衡状态, 以达到系统较好的“均衡”.两个最经典的迭代策略是“针锋相对” (Tit-for-tat, TFT)和“赢存输变” (Win-stay, lose-shift, WSFS). TFT策略:首先参与者不会背叛对方, 如果对手选择背叛, 在下一次博弈中他将选择背叛来惩罚对手; 如果下一次对手选择合作, 他将会和对手再次合作. WSFS策略:对收益设一个阈值, 当第一轮收益高于该值时, 在下一轮博弈时, 参与者将继续保持上一轮采取的策略; 如果上一轮所得收益低于该阈值, 则在下一轮博弈时, 参与者将采用与上一轮相反的策略.若11表示合作, 00表示背叛, TFT策略可表示为[1,0,1,0][1,0,1,0], WSFS策略表示为[1,0,0,1][1,0,0,1].

两人两策略的博弈除了囚徒困境, 当收益矩阵(2) 中的参数R, S, T, P满足不同条件时, 还有其他博弈类型.例如雪堆博弈(Snowdrift game, SG)、鹰鸽博弈(Hawk-dove game, HDG)、胆小鬼博弈(Chicken game, CG)等.

2 挖矿困境的博弈均衡分析

矿工正常挖矿, 会获得与其付出算力成正比的收益, 付出的算力会耗费大量的电力、人力、物力等资源; 矿工也可以通过只发送部分工作量证明进行区块截留攻击, 获得高于实际应获得的收益.攻击是最优策略, 但当所有矿工都选择这种策略时, 整个矿池的有效收益几乎为零, 所以矿工最终获得的收益少于不攻击时获得的收益.因此对于矿工而言, 攻击与否是一个困境.

2.1 相同算力的情形

在开放矿池中, 忠实矿工进行正常挖矿, 会耗费一定的算力, 假设耗费的资源为c (0＜c＜0)(0＜c＜0).矿工之间合作挖矿, 在一定程度上会增加挖到区块的概率, 并且各个矿工的期望收益也将大于单独进行挖矿时获得的收益.假设矿工合作挖矿时收益会扩大r (r>1)(r>1)倍, 系统将扩大后的收益再按算力进行公平分配.为了简单化模型, 假设每个矿工的算力相同, 扩大后的收益会进行平分.当矿工不忠实挖矿, 对该矿池进行区块截留攻击时, 矿池管理员仍会按其贡献算力分配收益, 这样的行为不仅使该矿池总收益减少, 所有矿工的收益也将降低, 这就是挖矿过程中的“搭便车者” (Free rider).这里只考虑矿池中有两个矿工的情况, 每个矿工有两种策略选择:合作(Cooperation, C)和攻击(Attack, A).假设每个矿工正常挖矿时的收益为1, 他们的收益情况如下所示:

CACA(r(1−c),12,r(1−c)12−c12−c,0,120)CACA(r(1−c),r(1−c)12−c,1212,12−c0,0)

当策略选择为(C, C)时, 两个矿工合作挖矿会扩大r倍收益, 也会耗费一定的资源c, 因此对应的收益为(r(1−c)(r(1−c), r(1−c))r(1−c)).当一个矿工选择合作, 另一个选择攻击时, 即(C, A)或(A, C), 对于合作者而言, 只有一个矿工进行挖矿, 收益不会被扩大r倍, 矿池收益为1, 忠实矿工和攻击者获得相同的收益1/21/2, 但忠实矿工正常挖矿会耗费其资源c, 所以其最终收益为1/2−c1/2−c, 攻击者收益为1/21/2.当两个矿工都选择攻击(A, A)时, 整个矿池的有效收益为0, 则这两个矿工的收益为0.

2.1.1 纯策略纳什均衡

当r(1−c)>1/2r(1−c)>1/2且c>1/2c>1/2, 一个矿工选择C策略时, 另一个矿工选择C策略比选择A策略获得收益大, 为了使自己的收益达到最大, 另一个矿工也会选择C策略; 当一个矿工选择A策略时, 另一个矿工选择C策略比选择A策略损失更多, 为了使自己的收益不损失太多, 另一个矿工只能选择A策略.因此, 在这种情况下, 矿工的纳什均衡点为(C, C), (A, A).在图 1中, 区域(c)满足该条件.

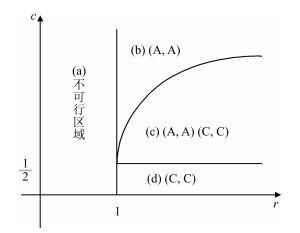图 1 矿工纯策略纳什均衡分布图Figure 1 The distribution of pure strategies Nash equilibrium for miners

当r(1−c)＜1/2r(1−c)＜1/2且c>1/2c>1/2, 一个矿工选择合作时, 另一个矿工会选择攻击来增加自己的收益; 当一个矿工选择攻击时, 为了不降低自己的收益, 另一个矿工只能选择攻击.也就是说, 无论对手选择何种策略, 矿工的最优策略是攻击, 这时矿工将面临矿工式的囚徒困境.此时的纳什均衡点为(A, A), 在图 1中, 表现为区域(b).

当r(1−c)>1/2r(1−c)>1/2且c＜1/2c＜1/2, 一个矿工选择合作时, 为了使自己的收益达到最高, 另一个矿工会选择合作; 当一个矿工选择攻击时, 为了使自己的收益不会损失很多, 另一个矿工仍旧会选择合作.即无论对手矿工选择何种策略, 该矿工选择合作对其自身利益是最大的.因此, 这时矿工的纳什均衡点为(C, C), 这种情况在图 1中为区域(d).

当r(1−c)＜1/2r(1−c)＜1/2且c＜1/2c＜1/2时, 有r＜1r＜1, 而r为收益扩大的倍数, 这与模型假设r>1r>1矛盾, 因此这种情况为图 1中的区域(a).

2.1.2 混合策略纳什均衡

矿工博弈有一个唯一的混合均衡点.设矿工1选择合作的概率为x (0≤x≤1)(0≤x≤1), 矿工2选择合作的概率为y (0≤y≤1)(0≤y≤1), 则矿工1合作的期望收益为y/2y/2, 矿工1攻击的期望收益为yr(1−c)+(1−y)(1/2−c)=ry−y/2−ryc+1/2−c+cyyr(1−c)+(1−y)(1/2−c)=ry−y/2−ryc+1/2−c+cy.在混合策略均衡点下, 矿工1合作与攻击的收益相等, 即

ry−y2−ryc+12−c+cy=y2ry−y2−ryc+12−c+cy=y2

化简后有

y=c−12(1−c)(r−1)y=c−12(1−c)(r−1)

(3)

同样地, 矿工2选择合作时的期望收益为xr(1xr(1 -c)+(1−x)(1/2−c)=rx−x/2−rxc+1/2c)+(1−x)(1/2−c)=rx−x/2−rxc+1/2 -c ++ cxcx.矿工2选择攻击时的期望收益为x/2x/2.在混合策略均衡下, 矿工2选择合作与攻击对应的收益也应是相等的, 即

rx−x2−rxc+12−c+cx=x2rx−x2−rxc+12−c+cx=x2

化简后有

x=c−12(1−c)(r−1)x=c−12(1−c)(r−1)

(4)

根据式(3) 和式(4) 可以得到混合均衡存在的条件

12≤c≤1−12r12≤c≤1−12r

(5)

定理1. 设算力相同的两个矿工合作的概率分别为x, y, 则x, y与挖矿资源耗费c成正比, 与合作后收益扩大倍数r成反比, 且混合策略均衡存在的条件为

12≤c≤1−12r12≤c≤1−12r

注1. 图 1中, 区域(b)和区域(d)只存在纯策略纳什均衡, 不满足不等式(5) 的条件约束.只有区域(c)满足不等式(5) 的条件约束, 即存在混合纳什均衡.

2.2 不同算力的情形

本节分析矿工算力不同时的系统分配收益情况.假设在开放矿池中有两个矿工挖矿, 整个矿池的总算力为1, 矿工1的算力为t (0＜t＜1)(0＜t＜1), 则另一个矿工的算力为(1−t)(1−t), 与上一个模型相同的是, c表示各种资源支出, r表示矿工合作后的收益扩大的倍数; 不同的是, 假设矿工挖矿后, 矿池的收益根据矿工挖矿情况而定, 资源支出c需满足c＜min(tc＜min(t, 1−t)1−t).不失一般性, 设t＜1−tt＜1−t, 这里仍然存在“搭便车"者:通过区块截留攻击, 增加自己的收益.矿工的策略选择仍然为C和A, 他们的收益情况如下:

CACA(r(t−c),t(1−t),r(1−t−c)(1−t)2−ct2−c,0,t(1−t)0)CACA(r(t−c),r(1−t−c)t2−c,t(1−t)t(1−t),(1−t)2−c0,0)

当两个矿工策略选择为(C, C)时, 合作挖矿时整个矿池收益为1, 矿工获得收益为自己的算力, 这样会耗费c, 但收益会扩大r倍, 因此这时的收益为(r(t−c)(r(t−c), r(1−t−c))r(1−t−c)), 当两个矿工策略选择为(C, A)时, 矿工1选择合作, 矿工2选择攻击, 这时整个矿池的收益为t, 矿工1获得收益为它所占整个矿池算力的比例与耗费资源之差, 即(t2−c)(t2−c).同样的, 矿工2的收益为t(1−t)t(1−t); 当两个矿工都选择攻击时, 系统有效收益为0, 此时每个矿工的收益也为0.

2.2.1 纯策略纳什均衡

1) 当r(t−c)>(1−t)tr(t−c)>(1−t)t, (1−t)2−c＜0(1−t)2−c＜0, 矿工1选择合作时, 矿工2为了获得更多的收益会选择合作:矿工1选择攻击时, 矿工2为了使自己的收益不会降低的太多也会选择攻击.因此这时矿工的纳什均衡点有两个: (C, C)和(A, A).

2) 当r(t−c)＜(1−t)tr(t−c)＜(1−t)t, (1−t)2−c>0(1−t)2−c>0, 矿工1选择攻击时, 矿工2为了有收益必须选择合作(当选择攻击时, 收益将为0), 此时的纳什均衡点为(A, C).

3) 当r(t−c)>(1−t)tr(t−c)>(1−t)t, (1−t)2−c>0(1−t)2−c>0或者t2t2 -c>0c>0时, 矿工1选择攻击, 另一个矿工选择合作时获得收益将高于选择攻击时获得的收益:而当矿工1选择合作时, 另一个矿工选择合作时的收益同样高于选择攻击时获得的.因此, 矿工的纳什均衡点为(C, C).

4) 当r(t−c)＜(1−t)tr(t−c)＜(1−t)t, (1−t)2−c＜0(1−t)2−c＜0时, 对手选择攻击, 该矿工选择合作时, 会获得较少收益, 当选择攻击时, 会获得相对多的收益.此时矿工的纳什均衡点为(A, A), 这就是矿工版的囚徒困境.

2.2.2 混合策略纳什均衡

矿工以某种概率进行策略选择, 当概率为0或1时, 存在纯策略纳什均衡, 当概率不为0或1时, 为混合策略均衡问题.假设矿工1合作的概率为x (0(0 ≤≤ x≤1)x≤1), 矿工2合作的概率为y (0≤y≤1)(0≤y≤1), 根据均衡的性质可以知, 矿工1选择是否合作, 收益应该是相等的, 即

yr(t−c)+(1−y)(t2−c)=yt(1−t)yr(t−c)+(1−y)(t2−c)=yt(1−t)

化简后为

y=c−t2(r−1)(t−c)y=c−t2(r−1)(t−c)

(6)

同样地, 均衡条件下, 矿工2选择攻击或合作的收益应该是相等的.即

xr(1−t−c)+(1−x)[(1−t)2−c]=xt(1−t)xr(1−t−c)+(1−x)[(1−t)2−c]=xt(1−t)

化简后为

x=c−(1−t)2(r−1)(1−t−c)x=c−(1−t)2(r−1)(1−t−c)

(7)

根据式(6) 和式(7), 可以得到在矿工算力不相同时混合均衡存在的条件

c>(1−t)2, r≥1+c−t2t−cc>(1−t)2, r≥1+c−t2t−c

(8)

定理2. 设算力不相同的两个矿工合作的概率分别为x, y, 则x, y与资源耗费c成正比, 与收益扩大倍数r成反比, 矿工的合作概率与其本身算力成反比, 且混合策略均衡存在的条件为

c>(1−t)2, r≥1+c−t2t−cc>(1−t)2, r≥1+c−t2t−c

注2. 根据x, y存在条件, 可以得出, 只有第1种和第4种情形的纯策略纳什均衡存在混合均衡.由此发现, 矿工算力相同是算力不同情况下的特殊情况.

3 挖矿困境的博弈优化

由第2节可知, 区域(c)的纳什均衡为(A, A), (C, C).当两个矿工相互攻击时, 将获得较低的系统收益, 甚至为零.为了提高矿池收益, 我们将ZD策略应用到该挖矿困境中, 对系统收益进行优化, 最终得到较高的收益.

具体模型如下:假设在一个开放矿池中, 有两类矿工, 一类忠实矿工(LM, 正常挖矿, 维护整个矿池的利益), 另一类自私矿工(SM, 自私挖矿, 只考虑自己的收益).对于(C, C)、(C, A)、(A, C)、(A, A)四种情况, LM和SM的混合策略概率分别为lm=lm= [a1[a1, a2a2, a3,a4]a3,a4]和sm=[b1,b2,b3,b4]sm=[b1,b2,b3,b4], lmlm, smsm分别是下一状态下选择合作的转移概率向量.例如, 上一状态两个矿工都选择C时, 下一状态LM选择C的概率为a1a1, 选择A的概率为(1−a1)(1−a1); SM选择C的概率为b1b1, 选择A的概率为(1−b1)(1−b1). LM的收益向量为

WWL= [RL,SL,TL,PL]T= [r(1−c),12−c,12,0]TWWL= [RL,SL,TL,PL]T= [r(1−c),12−c,12,0]T

SM的收益向量为

WWS= [RS,TS,SS,PS]T= [r(1−c),12,12−c,0]TWWS= [RS,TS,SS,PS]T= [r(1−c),12,12−c,0]T

因此, 两个矿工的策略选择转移情况可由马尔科夫状态转移矩阵M来表示.其中, 马尔科夫转移矩阵的稳态向量s=[s1,s2,s3,s4]Ts=[s1,s2,s3,s4]T, 且s1+s2+s3+s4s1+s2+s3+s4 = 11.

M=⎡⎣⎢⎢⎢⎢a1b1a2b3a3b2a4b4a1(1−b1)a2(1−b3)a3(1−b2)a4(1−b4)(1−a1)b1(1−a2)b3(1−a3)b2(1−a4)b4(1−a1)(1−b1)(1−a2)(1−b3)(1−a3)(1−b2)(1−a4)(1−b4)⎤⎦⎥⎥⎥⎥M=[a1b1a1(1−b1)(1−a1)b1(1−a1)(1−b1)a2b3a2(1−b3)(1−a2)b3(1−a2)(1−b3)a3b2a3(1−b2)(1−a3)b2(1−a3)(1−b2)a4b4a4(1−b4)(1−a4)b4(1−a4)(1−b4)]

ssTM=ssTssTM=ssT

(9)

则LM和SM的稳态期望收益分别为

UL=ssTWTUS=ssTWSUL=ssTWTUS=ssTWS

定义M′=M−IM′=M−I, 这里II是单位矩阵.因此式(9) 等价为

ssTM′=0ssTM′=0

根据克拉默法则, 可以得到

Adj(M′)M′=det(M′)I Adj(M′)M′=det(M′)I

其中, Adj(M′)(M′)为M′M′的伴随矩阵, 它的每一行都与ssss成比例.选取Adj(M′)(M′)的最后一行, 经过行列变换可以得到, 对于任意向量vv=[v1,v2,v3,v4]Tvv=[v1,v2,v3,v4]T, 与ssss的点积是一个行列式

sTv≡D(lm,sm,v)=sTv≡D(lm,sm,v)=

det⎡⎣⎢⎢⎢−1+a1b1a2b3a3b2a4b4−1+a1−1+a2a3a4−1+b1b3−1+b2b4v1v2v3v4⎤⎦⎥⎥⎥det[−1+a1b1−1+a1−1+b1v1a2b3−1+a2b3v2a3b2a3−1+b2v3a4b4a4b4v4]

假设vv=αWWL+βWS−γIvv=αWWL+βWS−γI, 这里αα, ββ是不为零的系统参数, 令lm′=[−1+a1,−1+a2,a3,a4]lm′=[−1+a1,−1+a2,a3,a4], 如果LM的混合策略lm′=ϕvv=ϕ(αWWL+βWWS−γI)lm′=ϕvv=ϕ(αWWL+βWWS−γI), 其中ϕϕ是不为零的次数, 则

αUL+βUS−γ=0αUL+βUS−γ=0

(10)

定理3. 在一个开放矿池中, 当LM采取ZD策略时, LM可以控制SM的收益与自己的收益保持线性关系: γ=αUL+βUSγ=αUL+βUS.

证明. 通过式(10) 可知, 无论SM采取哪种策略, LM都可以通过ZD策略使SM的收益与其自己收益保持线性关系.并且, 由于LM考虑系统的整体收益, 提高自身收益, 也将提高对手收益.

引理1. LM采取ZD策略时, 系统参数αα, ββ应满足

−1＜αβ＜0−1＜αβ＜0

(11)

γγ满足

γ≤min(αRL+βRS,αSL+βTS)γ≥max(αTL+βSS,αPL+βPS)γ≤min(αRL+βRS,αSL+βTS)γ≥max(αTL+βSS,αPL+βPS)

或者

γ≥max(αRL+βRS,αSL+βTS)γ≤min(αTL+βTS,αPL+βPS)γ≥max(αRL+βRS,αSL+βTS)γ≤min(αTL+βTS,αPL+βPS)

证明. 根据定理3可知, α/β＜0α/β＜0, 由式(10) 可得, LM的策略lmlm应满足

⎡⎣⎢⎢⎢a1−1a2−1a3a4⎤⎦⎥⎥⎥=ϕ⎡⎣⎢⎢⎢⎢αRL+βRS−γαSL+βTS−γαTL+βTS−γαPL+βPS−γ]⎤⎦⎥⎥⎥⎥[a1−1a2−1a3a4]=ϕ[αRL+βRS−γαSL+βTS−γαTL+βTS−γαPL+βPS−γ]]

(12)

混合策略概率aiai (i=1,2,3,4)(i=1,2,3,4)应该满足0≤ai0≤ai ≤1≤1, 有

−1−100≤ϕ(αRL+βRS−γ)≤0≤ϕ(αSL+βTS−γ)≤0≤ϕ(αTL+βSS−γ)≤1≤ϕ(αPL+βPS−γ)≤1−1≤ϕ(αRL+βRS−γ)≤0−1≤ϕ(αSL+βTS−γ)≤00≤ϕ(αTL+βSS−γ)≤10≤ϕ(αPL+βPS−γ)≤1

(13)

根据不等式组(13), 当ϕ＜0ϕ＜0时, γγ需满足

γ≤min(αRL+βRS,αSL+βTS)γ≥max(αTL+βSS,αPL+βPS)γ≤min(αRL+βRS,αSL+βTS)γ≥max(αTL+βSS,αPL+βPS)

(14)

在挖矿过程中, 很明显SL=SS＜TS=TLSL=SS＜TS=TL, 对于这种情况不失一般性, 假设α>0α>0, β＜0β＜0, 则

αSL+βTS≤αTL+βSSαSL+βTS≤αTL+βSS

(15)

很明显, 式(15) 与式(14) 矛盾.

根据式(13), 当ϕ>0ϕ>0时, γγ需满足:

γ≥max(αRL+βRS,αSL+βTS)γ≤min(αTL+βSS,αPL+βPS)γ≥max(αRL+βRS,αSL+βTS)γ≤min(αTL+βSS,αPL+βPS)

(16)

由式(16) 可以得到系数αα和ββ应满足:

αRL+βRS≤αPL+βPSαRL+βRS≤αPL+βPS

(17)

即

αβ>PS−RSRL−PL=−1αβ>PS−RSRL−PL=−1

(18)

当α＜0α＜0, β＜0β＜0时, 可以得到条件与式(16) 矛盾, 通过式(14) 仍然可以得到α/β>−1α/β>−1.

综上分析, 当LM采取ZD策略时, 即lm′=ϕvvlm′=ϕvv = ϕ(αWWL+βWWS−γI)ϕ(αWWL+βWWS−γI).可以得到系统参数αα, ββ应满足式(11).

定理4. 在挖矿过程中, 当LM采取ZD策略, 满足γ=αUL+βUSγ=αUL+βUS和α/β＜0α/β＜0时, 两个矿工的最终收益可以为图 2上线段ACAC和AFAF上的任意一点, 并且LM可以用ZD策略单方面控制线段AC.在A点可以使该模型达到一个新的纳什均衡---这个均衡具有较高的系统收益, 即: UL(lm∗,sm∗)UL(lm∗,sm∗) ++ US(lm∗,sm∗)US(lm∗,sm∗), 并且LM和SM不会偏离这个均衡, 即:

UL(lm∗,sm∗)+US(lm∗,sm∗)≥UL(lm,sm∗)+US(lm,sm∗)UL(lm∗,sm∗)+US(lm∗,sm∗)≥UL(lm∗,sm)+US(lm∗,sm)UL(lm∗,sm∗)+US(lm∗,sm∗)≥UL(lm,sm∗)+US(lm,sm∗)UL(lm∗,sm∗)+US(lm∗,sm∗)≥UL(lm∗,sm)+US(lm∗,sm)

LM的ZD策略lm∗lm∗为

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪a1=1a2=1+ϕ(α(SL−TL)+β(TS−RS))a3=ϕ(α(TL−RL)+β(SS−RS))a4=ϕ(α(PL−RL)+β(PS−RS)){a1=1a2=1+ϕ(α(SL−TL)+β(TS−RS))a3=ϕ(α(TL−RL)+β(SS−RS))a4=ϕ(α(PL−RL)+β(PS−RS))

(19)

证明. 下面对矿工算力不相同时, 对纯策略纳什均衡中的第4种情况进行证明, 即满足r(t−c)＜r(t−c)＜ (1−t)t(1−t)t, (1−t)2−c＜0(1−t)2−c＜0条件, 纳什均衡为(A, A).则该情形下, 两个矿工的收益(UL′,US′)(UL′,US′)分布为图 2中四边形ABECABEC, 不失一般性, 假设α>0α>0, β＜0β＜0.当γ=αUL′+βUS′γ=αUL′+βUS′时, 则LM可以通过采取ZD策略控制线性关系α(RL−UL′)+β(RS−US′)=0α(RL−UL′)+β(RS−US′)=0.

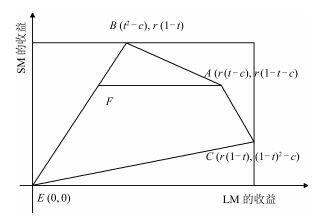图 2 算力不同时矿工的收益分布情况Figure 2 The payoff distribution of miners with different powers

下面分析当矿工收益为四边形ABECABEC各区域时, 矿工挖矿博弈的不同结果, 以及最优区域.

当UL′＜RLUL′＜RL, US′＜RSUS′＜RS时, 也就是图 2中的三角形ABFABF区域, 有γ=αUL′+βUS′>αRL+βRSγ=αUL′+βUS′>αRL+βRS, 这与式(16) 矛盾.因此, 当UL′＜RLUL′＜RL, US′＜RSUS′＜RS时, LM不能采取ZD策略满足两个收益的线性关系式α(RL−UL′)+β(RS−US′)=0α(RL−UL′)+β(RS−US′)=0.也就是说当LM采取ZD策略时, 矿工挖矿博弈结果是不会优于矿工收益为四边形AFECAFEC时所得到的收益.

收益分布在线段FAFA.当LM的ZD策略lm′=ϕ(αWWL+βWWS−γI)lm′=ϕ(αWWL+βWWS−γI)中的α=0α=0时, 可以满足γγ = βUSβUS, 并且满足式(15).这时, SM的收益都在线段FAFA上.即, 当LM采取ZD策略时, 不管SM采取何种策略, LM都可以控制SM的收益为线段FAFA上的任意一点, 并且可以保持两个矿工收益的线性关系值不变.

同样的, 可以得到在线段ACAC上, LM采取ZD策略时, 即可以保持两个矿工收益的线性关系.而在线段CECE上并不能保持该线性关系.

综上分析, 可以得到当两个矿工最终受益可以为FAFA和ACAC上的任意一点.对于线段ACAC, 不管SM采取何种策略, LM都可以通过调整α/βα/β的值单方面控制两个矿工的收益.

不失一般性, 假设α>0α>0, β＜0β＜0, 当ϕ>0ϕ>0时, 对于任意的αα和ββ, 只有满足式(11), 并且γ=RLγ=RL ++ RSRS, 则LM采取的ZD策略lm∗lm∗ (式(19))可以由式(12) 得到, 即, 不管SM采取何种策略, LM可以单方面控制两个矿工收益的线性关系, 并且系统收益可以达到较高值.

注3. 定理4从博弈论的角度对PoW共识算法中矿工的策略选择进行优化, 给出系统达到较高收益时的均衡条件.即采用ZD策略方法使系统丢弃原来挖矿困境相互攻击的纳什均衡, 形成新的均衡, 从而提高系统的整体收益.所以, 基于ZD策略的博弈论方法为设计高效的共识算法提供新的思路和研究方法.

4 数值仿真及结果分析

基于上述模型, 用数值仿真来说明LM用ZD策略(lm′=ϕ(αWWL+βWWS−γI)lm′=ϕ(αWWL+βWWS−γI), γ=αUL+βUSγ=αUL+βUS)可以使LM和SM的收益保持线性关系, 并且维持系统收益稳定并达到一定的高度.当矿工算力相同时, 假设系统参数资源耗费c=5/8c=5/8, 合作后矿工收益扩大倍数r=5/3r=5/3, ϕ=1/20ϕ=1/20, α=8α=8, β=−18β=−18. LM和SM的收益向量分别为WWL=[5/8,−1/8,1/2,0]TWWL=[5/8,−1/8,1/2,0]T, WWSWWS =[5/8,1/2,−1/8,0]T=[5/8,1/2,−1/8,0]T.

下面是当LM和SM分别采取不同策略时, 对系统收益的分析.其中, WSFS策略的混合策略概率为[1,0,0,1][1,0,0,1], TFT策略的混合策略概率为[1,0,1[1,0,1, 0]0].

在图 3中, 当SM采取WSFS策略时, LM选择ZD或者WSFS策略时, 最终系统收益能达到最优值1.25, 而LM采取TFT策略或一个随机策略[0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4]时, 系统收益不能达到最优.通过比较可以发现, 在LM选择的这4种策略中, WSFS策略是最佳选择, ZD策略经过迭代一定次数后也能达到系统最优, 而TFT策略和随机策略[0.1,0.2[0.1,0.2, 0.3,0.4]0.3,0.4]都只能获得较低的系统收益.

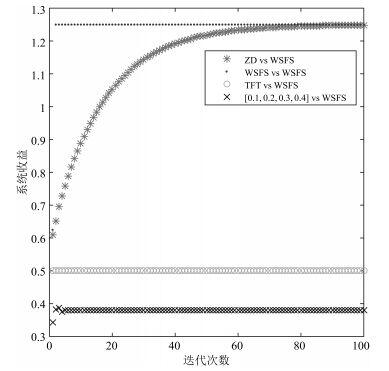图 3 当矿工算力相同时, LM采用不同策略, SM始终采用WSFS策略后, 系统收益分布情况Figure 3 The distribution of systematic revenue, when LM takes different strategies and SM all uses WSFS strategy in the condition of same power

在图 4中, SM采用TFT策略, LM分别采取ZD、WSFS、TFT、[0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4]四种策略.观察图 3, 通过对比发现这4种博弈都不能使系统达到最优, 而ZD策略虽然不能系统收益最优, 但相对于其他策略有明显的优势, 在迭代一定次数后可以使系统收益趋向于稳定, 并且可以得到高于其他策略的收益. LM的最差策略为随机策略[0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4].

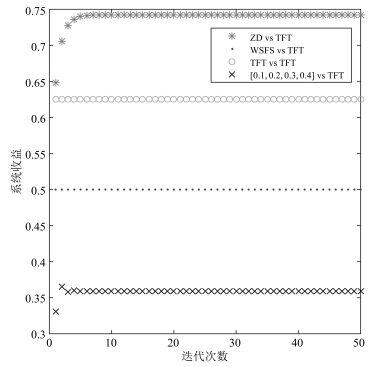图 4 当矿工算力相同时, LM采用不同策略, SM始终采用TFT策略后, 系统收益分布情况Figure 4 The distribution of systematic revenue, when LM takes different strategies and SM all uses TFT strategy in the condition of same power

在图 5中, SM始终选择[0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4]策略, LM仍然采取ZD、WSFS、TFT、[0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4]四种策略.这4种博弈同样不能达到最优, 当LM采取ZD策略时, 经过一定次数的迭代博弈后, 系统收益逐渐稳定并且明显高于其他3个策略.这时, SM最不可取的策略为TFT策略.

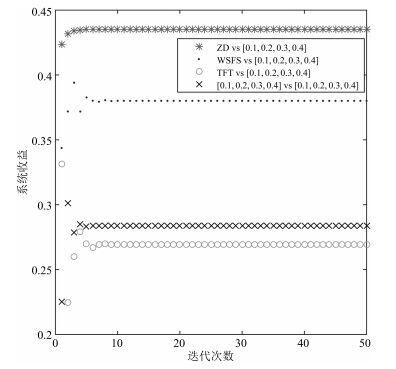图 5 当矿工算力相同时, LM采用不同策略, SM始终采用[0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4]策略后, 系统收益分布情况Figure 5 The distribution of systematic revenue, when LM takes different strategies and SM all uses [0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4] strategy in the condition of same power

根据图 6可以得到, 不论SM选择何种策略, 只要LM采用ZD策略, 两个矿工收益的线性组γ=γ= αULαUL ++ βUSβUS, 随着迭代次数的增加, 会逐渐趋向稳定, 并且都为同一个值.也就是说, 当矿工算力相同时, LM可以用ZD策略控制SM的收益与自己收益保持线性关系, 不论SM采取何种策略.

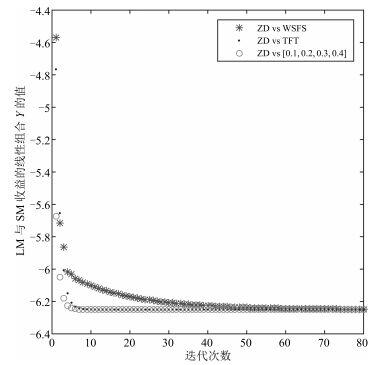图 6 当矿工算力相同时, LM采用ZD策略, SM采用不同的三种策略, LM和SM收益的线性关系Figure 6 The linear relationship between LM′′ payoff and SM′′ payoff, when LM takes a ZD strategies and SM uses three different strategy in the condition of same power

当矿工算力不同时, 参数满足不同的条件, 也会有不同的困境.当系统条件满足纯策略中的第4种(均衡点为双攻击)情形时, 我们对该情形进行建模, 不妨假设参数ϕ=1/20ϕ=1/20, α=1α=1, β=−10β=−10, 算力耗费c=0.3c=0.3, 收益扩大倍数r=1.1r=1.1, LM的算力t=t= 0.480.48, 则SM的算力(1−t)=0.52(1−t)=0.52.

在图 7中, SM采用WSFS策略, LM分别采用ZD、WSFS、TFT、[0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4]策略. LM采用WSFS能立即使系统收益达到最优, 而采用ZD策略后, 在迭代一定次数后也能使系统收益得到满足.另外两种策略只能使系统收益处于较低值.在这4种策略中, 最差的为随机策略[0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4].

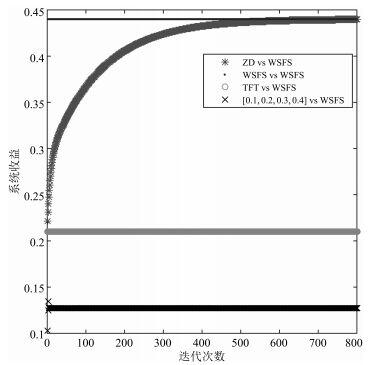图 7 当矿工算力不相同时, SM采用WSFS策略, LM采用不同的四种策略, 系统收益情况Figure 7 The distribution of systematic revenue, when SM all uses WSFS strategy and LM takes different four strategies and in the condition of different power

图 8与图 7不同的是, 这里的SM采取的是TFT策略.从图 8可以发现, 虽然ZD策略不能使系统收益达到最优, 但它仍然是LM的最佳选择, 在重复一定次数后, 系统收益可以达到稳定, 并优于其他3个策略, 其他3个策略只能使系统收益更低.这里的劣势策略仍然为[0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4].

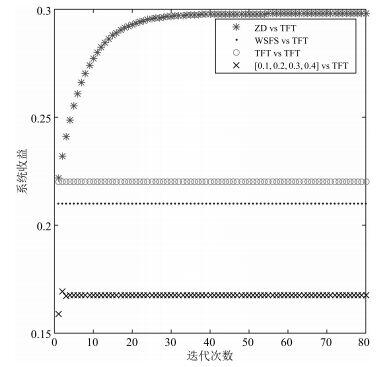图 8 当矿工算力不相同时, SM采用TFT策略, LM采用不同的四种策略, 系统收益情况Figure 8 The distribution of systematic revenue, when SM all uses TFT strategy and LM takes different four strategies and in the condition of different power

在图 9中, LM同样采用4种不同的策略, 这4种策略都不能使系统收益达到最高, 但比较这4种策略, ZD策略对应的系统收益要明显高于其他3种策略, 这说明ZD是LM的最佳选择, 而TFT策略则是最不可取的策略.

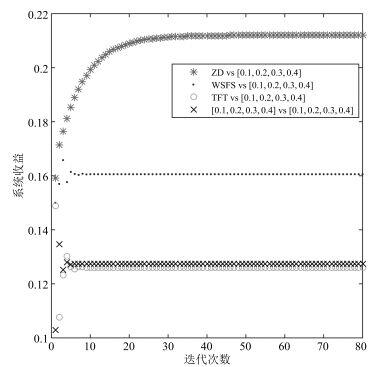图 9 当矿工算力不相同时, SM采用[0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4]策略, LM采用不同的四种策略, 系统收益情况Figure 9 The distribution of systematic revenue, when SM all uses [0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4] strategy and LM takes different four strategies and in the condition of different power

图 10为LM采用ZD策略, SM分别采取其他3种策略.从图 10可以看出, 随着迭代次数的增加, LM和SM收益的线性组合γ=αUL+βUSγ=αUL+βUS, 会逐渐稳定到同一值, 由此验证了我们的结论:当矿工算力不同时, 不论SM采取何种策略, LM都可以通过采用ZD策略, 使两个矿工的收益保持线性关系.

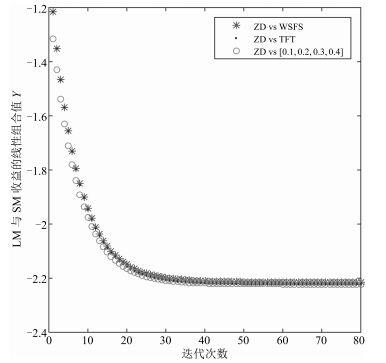图 10 当矿工算力不相同时, LM采用ZD策略, SM采用不同的三种策略, LM和SM收益的线性关系Figure 10 The linear relationship between LM′′ payoff and SM′′ payoff, when LM takes a ZD strategies and SM uses three different strategy in the condition of different power

综合以上分析, 可以得到下面的结论:无论矿工算力是否相同, 无论SM采取何种策略, 当LM采用ZD策略时, 经过一定次数的重复博弈, 可以获得相对高的系统收益, 甚至能达到最优.并且无论SM选择哪种策略, 经过一定次数的迭代, LM都可以使SM的收益与自己的收益保持线性关系, 这使得设计高效的博弈共识算法成为可能.

5 总结与展望

一方面, 均衡分析是博弈论中的一块重要内容.本文对共识算法挖矿困境的分析, 对理解和剖析PoW共识算法本身具有一定的理论参考价值.具体地, 当矿工算力相同时, 3种情况的纯策略纳什均衡分为(A, A), (C, C)和(A, A), (C, C).对于混合策略均衡, 给出均衡存在条件, 并得到两个重要结论: 1) 当收益扩大倍数r不变时, 资源耗费c与合作概率成正比; 2) 当c不变时, 收益扩大倍数r与合作概率成反比.当矿工算力不相同时, 根据参数满足不同的条件, 可以将此时的困境分为4种, 纯策略纳什均衡分别为(A, A), (C, C), (A, A)和(C, C), (A, C).通过分析得到混合策略均衡存在条件, 以及一个重要结论:当收益扩大倍数r和费用支出c保持不变时, 矿工的算力与合作的概率成反比.这些性质, 对矿工挖矿的均衡选择起到理论指导意义.

另一方面, 有效共识机制的设计一直是区块链技术的核心问题.在PoW共识算法中正常挖矿的纳什均衡是相互攻击, 给系统本身造成资源浪费.本文应用ZD策略对PoW共识算法中矿工的策略选择进行优化, 使得系统收益达到最大化, 为进一步设计基于博弈论的高效共识算法提供了新的研究思路和方法.具体地, 对PoW共识过程中矿工的策略选择进行优化, 发现LM采取ZD策略, 可以使系统收益达到较高值, 甚至控制系统收益, 使之达到最优, 也可以使SM的收益与自己的收益保持线性关系, 并给出数值仿真, 进一步说明结论的正确性.

此外, 以太坊中的PoS共识算法中也存在类似的策略选择困境:权益较大者忠实于矿池是否能获得高收益, 权益较小者忠实于矿池是否一定能维护自己的权益并获得相应收益.后续工作将对这种情况及区块链中类似模型进行分析, 通过对系统均衡的分析, 设计更合理更有效的共识机制.