一种基于 Schnoor 算法的多签方案以及钱包架构

硬核预警，建议有技术基础的同学使用～

近日比特币核心客户端发布了新的一个大版本，这次发布主要带来了 Schnorr 签名 Taproot 技术。Schnorr 是一项优雅，简洁，可以提升交易隐私性，节省空间，同时还能实现聚合多签的一种的签名算法。同时它有别于传统的 ESDSA 签名技术，其在技术及实现方式上有着明显的特点，目前已经较广泛的应用在不同公链的不同环节上。本期非常有幸邀请到密码学专家汉升（笔名）撰稿，介绍一种基于 Schnoor 算法的多签方案以及钱包架构。同时在文末为大家推荐了两篇相关科普文章，希望能够一起学习这一项新的技术，以及了解 Schnorr 签名对于比特币及区块链技术的发展有哪些意义。

ECDSA签名回顾  

数字签名是对签名的数字模拟。最早的数字签名算法是由Rivest、Shamir、Adleman三⼈于1978年提出的RSA签名算法，其安全性基于⼤整数分解的难解性，⼴泛地运⽤于数字认证与CA等领域。但是由于RSA算法的密钥尺⼨较⼤，存储效率不及后来的基于椭圆曲线的签名算法。所以⽬前⼴泛运⽤于密码货币的签名⼏乎都是ECDSA算法，只是所基于的底层椭圆曲线不同。ECDSA的安全性是基于椭圆曲线离散对数难解性。

⽐特币签名算法——

基于 SECP256k1 曲线的ECDSA

⽐特币⽬前所使⽤的签名算法是基于SECP256k1 曲线的ECDSA算法。将交易的详细信息 作消息摘要， 即 z=SHA256(m)，对摘要z作核⼼签名算法。

密码学意义上安全的数字签名需要通过添加随机数来实现签名的随机性。但是根据RFC6979标准，签名 算法中的随机数是从消息摘要z中提取出，这不是密码学意义上的随机数。这个⽅案在众多密码学代码库中，并应⽤于⼤多数区块链项⽬中。

Schnorr签名的平凡⽅案

Schnorr签名可以解决上⾯所提出的多签消耗资源的问题。

Schnorr是由Claus-Peter Schnorr在1989年美密会上提出的数字签名算法，并申请了专利保护。就签名算法本身⽽⾔，它相对于ECDSA算法具有，可证明安全性、可扩展性的特点。

主要算法实现如下：

可以看出Schnorr签名也基于椭圆曲线算术，⽬前⼴泛部署于各⼤代码库、芯⽚指令中的底层算术模块依 

然可以有效利⽤，但是需要将再重新从底层接⼝封装指令来实现Schnorr算法。这点对于软件钱包升级⽐ 较便利。但是对于硬件钱包，升级成本可能较⾼。 

Schnorr签名⽅案的线性性质

假设Alice和Bob分别对于消息m进⾏签名。具体地，假设Alice的公私钥对为(x1,X1=x1G) ，Bob的公私 (x2,X2=x2G),

以上的⽅案只是为了展示Schnorr签名的线性性，并不能直接⽤于实际应⽤，因为这个⽅案可能会导致 Rouge key Attack。 

基于Schnorr签名的多签⽅案

多签⽅案

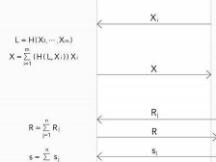
以n-of-m多签⽅案为例。

钱包服务架构

钱包分为服务器端(S端)和客户端(C端)，C端将有多个逻辑点，对应多个⽤户。

这⾥的S端和C端只是逻辑上的，可以在⼀个物理设备上既有S端也有C端，也可能是多个物理设备上的。 

结论

对于Schnorr的线性性质以及签名可累积性质，使得在⽐特币多签交易的执⾏中，不需要过多的⽤户签名数据，只需要"签名和"与"公钥和"即可验证交易合法性。这会让⽐特币的多签交易⼤⼩⼤幅降低，从⽽区块能容纳的多签交易数量得到较⼤提⾼。以2-3多签为例，⽬前⽐特币多签的锁定脚本需要3个公钥地址，这部分会被压缩为脚本，所以升级之后⼤⼩⽆变化，但是解锁脚本需要2个公钥与2个签名，在升级为Schnorr之后，只需要⼀个"公钥和"与"签名和"。对于更通⽤的n-m多签，⽬前⽐特币多签的解锁脚本需要n个公钥与n个签名，Schnorr签名依然只需要⼀个"公钥和"与⼀个"签名和”。也就是说签名⼈越多，Schnorr签名的空间利⽤率越⾼。